Data Structure and Algorithm

Complied by Linh Truong | Incomplete and will be updated

1 Data Structure................................................................................................................................. 1

1.1 Hash Table................................................................................................................................ 3

1.2 Dynamic Array.......................................................................................................................... 7

1.3 Linked List............................................................................................................................... 11

1.4 Stacks..................................................................................................................................... 15

1.5 Queues................................................................................................................................... 15

1.6 Set.......................................................................................................................................... 15

1.7 TreeSet................................................................................................................................... 18

1.8 Binary Search Tree (BST).......................................................................................................... 20

1.9 Heap (Max Heap/Min Heap).................................................................................................... 25

1.10 Graph................................................................................................................................... 35

2 Algorithms..................................................................................................................................... 46

2.1 Sorting.................................................................................................................................... 48

2.2 Searching................................................................................................................................ 48

2.3 Tree Traversals........................................................................................................................ 48

2.4 Breadth-First Search................................................................................................................ 55

2.5 Depth-First Search................................................................................................................... 59

2.6 Binary Search.......................................................................................................................... 64

3 Concepts....................................................................................................................................... 66

3.1 Bit Manipulation..................................................................................................................... 66

3.2 Memory (Stack VS. Heap)........................................................................................................ 66

3.3 Recursion................................................................................................................................ 66

3.4 Dynamic Programming............................................................................................................ 66

3.5 Big 0 Time & Space.................................................................................................................. 66

1 Data Structure

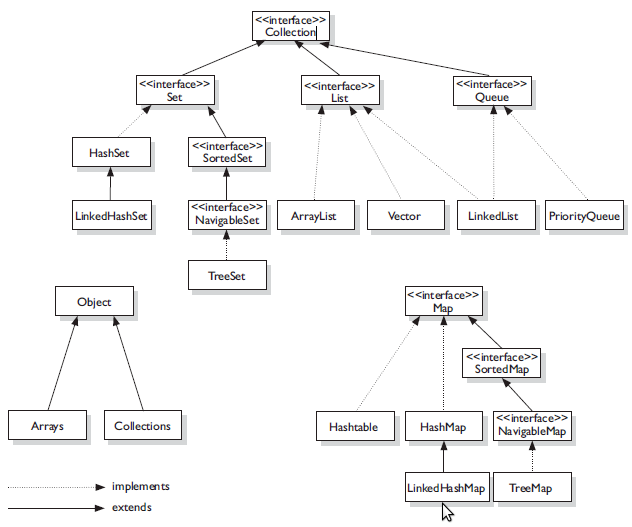
Java Collection Framework cheat sheet

A collection is a data structure—actually, an object—that can hold references to other objects. Usually, collections contain references to objects that are all of the same type. The collections-framework interfaces declare the operations to be performed generically on various types of collections.

Interface	Description
Collection	The root interface in the collections hierarchy from which interfaces Set, Queue and List are derived.
Set	A collection that does not contain duplicates.
List	An ordered collection that can contain duplicate elements.
Map	A collection that associates keys to values and cannot contain duplicate keys.
Queue	Typically a first-in, first-out collection that models a waiting line; other orders can be specified.

1.1 Hash Table

Hashtable was part of the original java.util and is a concrete implementation of a Dictionary.

However, Java 2 re-engineered Hashtable so that it also implements the Map interface. Thus, Hashtable is now integrated into the collections framework. It is similar to HashMap, but is synchronized.

Like HashMap, Hashtable stores key/value pairs in a hash table. When using a Hashtable, you specify an object that is used as a key, and the value that you want linked to that key. The key is then hashed, and the resulting hash code is used as the index at which the value is stored within the table.

Following is the list of constructors provided by the HashTable class.

Sr.No	Constructor & Description
1	Hashtable( ) This is the default constructor of the hash table it instantiates the Hashtable class.
2	Hashtable(int size) This constructor accepts an integer parameter and creates a hash table that has an initial size specified by integer value size.
3	Hashtable(int size, float fillRatio) This creates a hash table that has an initial size specified by size and a fill ratio specified by fillRatio. This ratio must be between 0.0 and 1.0, and it determines how full the hash table can be before it is resized upward.
4	Hashtable(Map < ? extends K, ? extends V > t) This constructs a Hashtable with the given mappings.

Apart from the methods defined by Map interface, Hashtable defines the following methods −

Sr.No	Method & Description
1	void clear( ) Resets and empties the hash table.
2	Object clone( ) Returns a duplicate of the invoking object.
3	boolean contains(Object value) Returns true if some value equal to the value exists within the hash table. Returns false if the value isn't found.
4	boolean containsKey(Object key) Returns true if some key equal to the key exists within the hash table. Returns false if the key isn't found.
5	boolean containsValue(Object value) Returns true if some value equal to the value exists within the hash table. Returns false if the value isn't found.
6	Enumeration elements( ) Returns an enumeration of the values contained in the hash table.
7	Object get(Object key) Returns the object that contains the value associated with the key. If the key is not in the hash table, a null object is returned.
8	boolean isEmpty( ) Returns true if the hash table is empty; returns false if it contains at least one key.
9	Enumeration keys( ) Returns an enumeration of the keys contained in the hash table.
10	Object put(Object key, Object value) Inserts a key and a value into the hash table. Returns null if the key isn't already in the hash table; returns the previous value associated with the key if the key is already in the hash table.
11	void rehash( ) Increases the size of the hash table and rehashes all of its keys.
12	Object remove(Object key) Removes the key and its value. Returns the value associated with the key. If the key is not in the hash table, a null object is returned.
13	int size( ) Returns the number of entries in the hash table.
14	String toString( ) Returns the string equivalent of a hash table.

Example

The following program illustrates several of the methods supported by this data structure −

Live Demo

import java.util.*;

public class HashTableDemo {

public static void main(String args[]) {

// Create a hash map

Hashtable balance = new Hashtable();

Enumeration names;

String str;

double bal;

balance.put("Zara", new Double(3434.34));

balance.put("Mahnaz", new Double(123.22));

balance.put("Ayan", new Double(1378.00));

balance.put("Daisy", new Double(99.22));

balance.put("Qadir", new Double(-19.08));

// Show all balances in hash table.

names = balance.keys();

while(names.hasMoreElements()) {

str = (String) names.nextElement();

System.out.println(str + ": " + balance.get(str));

}

System.out.println();

// Deposit 1,000 into Zara's account

bal = ((Double)balance.get("Zara")).doubleValue();

balance.put("Zara", new Double(bal + 1000));

System.out.println("Zara's new balance: " + balance.get("Zara"));

}

This will produce the following result −

Output

Qadir: -19.08

Zara: 3434.34

Mahnaz: 123.22

Daisy: 99.22

Ayan: 1378.0

Zara's new balance: 4434.34

1.2 Dynamic Array

The ArrayList class extends AbstractList and implements the List interface. ArrayList supports dynamic arrays that can grow as needed.

Standard Java arrays are of a fixed length. After arrays are created, they cannot grow or shrink, which means that you must know in advance how many elements an array will hold.

Array lists are created with an initial size. When this size is exceeded, the collection is automatically enlarged. When objects are removed, the array may be shrunk.

Following is the list of the constructors provided by the ArrayList class.

Sr.No.	Constructor & Description
1	ArrayList( ) This constructor builds an empty array list.
2	ArrayList(Collection c) This constructor builds an array list that is initialized with the elements of the collection c.
3	ArrayList(int capacity) This constructor builds an array list that has the specified initial capacity. The capacity is the size of the underlying array that is used to store the elements. The capacity grows automatically as elements are added to an array list.

Apart from the methods inherited from its parent classes, ArrayList defines the following methods −

Sr.No.	Method & Description
1	void add(int index, Object element) Inserts the specified element at the specified position index in this list. Throws IndexOutOfBoundsException if the specified index is out of range (index < 0 \|\| index > size()).
2	boolean add(Object o) Appends the specified element to the end of this list.
3	boolean addAll(Collection c) Appends all of the elements in the specified collection to the end of this list, in the order that they are returned by the specified collection's iterator. Throws NullPointerException, if the specified collection is null.
4	boolean addAll(int index, Collection c) Inserts all of the elements in the specified collection into this list, starting at the specified position. Throws NullPointerException if the specified collection is null.
5	void clear() Removes all of the elements from this list.
6	Object clone() Returns a shallow copy of this ArrayList.
7	boolean contains(Object o) Returns true if this list contains the specified element. More formally, returns true if and only if this list contains at least one element e such that (o==null ? e==null : o.equals(e)).
8	void ensureCapacity(int minCapacity) Increases the capacity of this ArrayList instance, if necessary, to ensure that it can hold at least the number of elements specified by the minimum capacity argument.
9	Object get(int index) Returns the element at the specified position in this list. Throws IndexOutOfBoundsException if the specified index is out of range (index < 0 \|\| index >= size()).
10	int indexOf(Object o) Returns the index in this list of the first occurrence of the specified element, or -1 if the List does not contain this element.
11	int lastIndexOf(Object o) Returns the index in this list of the last occurrence of the specified element, or -1 if the list does not contain this element.
12	Object remove(int index) Removes the element at the specified position in this list. Throws IndexOutOfBoundsException if the index out is of range (index < 0 \|\| index >= size()).
13	protected void removeRange(int fromIndex, int toIndex) Removes from this List all of the elements whose index is between fromIndex, inclusive and toIndex, exclusive.
14	Object set(int index, Object element) Replaces the element at the specified position in this list with the specified element. Throws IndexOutOfBoundsException if the specified index is out of range (index < 0 \|\| index >= size()).
15	int size() Returns the number of elements in this list.
16	Object[] toArray() Returns an array containing all of the elements in this list in the correct order. Throws NullPointerException if the specified array is null.
17	Object[] toArray(Object[] a) Returns an array containing all of the elements in this list in the correct order; the runtime type of the returned array is that of the specified array.
18	void trimToSize() Trims the capacity of this ArrayList instance to be the list's current size.

Example

The following program illustrates several of the methods supported by ArrayList −

Live Demo

import java.util.*;

public class ArrayListDemo {

public static void main(String args[]) {

// create an array list

ArrayList al = new ArrayList();

System.out.println("Initial size of al: " + al.size());

// add elements to the array list

al.add("C");

al.add("A");

al.add("E");

al.add("B");

al.add("D");

al.add("F");

al.add(1, "A2");

System.out.println("Size of al after additions: " + al.size());

// display the array list

System.out.println("Contents of al: " + al);

// Remove elements from the array list

al.remove("F");

al.remove(2);

System.out.println("Size of al after deletions: " + al.size());

System.out.println("Contents of al: " + al);

}

This will produce the following result −

Output

Initial size of al: 0

Size of al after additions: 7

Contents of al: [C, A2, A, E, B, D, F]

Size of al after deletions: 5

Contents of al: [C, A2, E, B, D]

1.3 Linked List

The LinkedList class extends AbstractSequentialList and implements the List interface. It provides a linked-list data structure.

Following are the constructors supported by the LinkedList class.

Sr.No.

Constructor & Description

LinkedList( )

This constructor builds an empty linked list.

LinkedList(Collection c)

This constructor builds a linked list that is initialized with the elements of the collection c.

Apart from the methods inherited from its parent classes, LinkedList defines following methods −

Sr.No.	Method & Description
1	void add(int index, Object element) Inserts the specified element at the specified position index in this list. Throws IndexOutOfBoundsException if the specified index is out of range (index < 0 \|\| index > size()).
2	boolean add(Object o) Appends the specified element to the end of this list.
3	boolean addAll(Collection c) Appends all of the elements in the specified collection to the end of this list, in the order that they are returned by the specified collection's iterator. Throws NullPointerException if the specified collection is null.
4	boolean addAll(int index, Collection c) Inserts all of the elements in the specified collection into this list, starting at the specified position. Throws NullPointerException if the specified collection is null.
5	void addFirst(Object o) Inserts the given element at the beginning of this list.
6	void addLast(Object o) Appends the given element to the end of this list.
7	void clear() Removes all of the elements from this list.
8	Object clone() Returns a shallow copy of this LinkedList.
9	boolean contains(Object o) Returns true if this list contains the specified element. More formally, returns true if and only if this list contains at least one element e such that (o==null ? e==null : o.equals(e)).
10	Object get(int index) Returns the element at the specified position in this list. Throws IndexOutOfBoundsException if the specified index is out of range (index < 0 \|\| index >= size()).
11	Object getFirst() Returns the first element in this list. Throws NoSuchElementException if this list is empty.
12	Object getLast() Returns the last element in this list. Throws NoSuchElementException if this list is empty.
13	int indexOf(Object o) Returns the index in this list of the first occurrence of the specified element, or -1 if the list does not contain this element.
14	int lastIndexOf(Object o) Returns the index in this list of the last occurrence of the specified element, or -1 if the list does not contain this element.
15	ListIterator listIterator(int index) Returns a list-iterator of the elements in this list (in proper sequence), starting at the specified position in the list. Throws IndexOutOfBoundsException if the specified index is out of range (index < 0 \|\| index >= size()).
16	Object remove(int index) Removes the element at the specified position in this list. Throws NoSuchElementException if this list is empty.
17	boolean remove(Object o) Removes the first occurrence of the specified element in this list. Throws NoSuchElementException if this list is empty. Throws IndexOutOfBoundsException if the specified index is out of range (index < 0 \|\| index >= size()).
18	Object removeFirst() Removes and returns the first element from this list. Throws NoSuchElementException if this list is empty.
19	Object removeLast() Removes and returns the last element from this list. Throws NoSuchElementException if this list is empty.
20	Object set(int index, Object element) Replaces the element at the specified position in this list with the specified element. Throws IndexOutOfBoundsException if the specified index is out of range (index < 0 \|\| index >= size()).
21	int size() Returns the number of elements in this list.
22	Object[] toArray() Returns an array containing all of the elements in this list in the correct order. Throws NullPointerException if the specified array is null.
23	Object[] toArray(Object[] a) Returns an array containing all of the elements in this list in the correct order; the runtime type of the returned array is that of the specified array.

Example

The following program illustrates several of the methods supported by LinkedList −

Live Demo

import java.util.*;

public class LinkedListDemo {

public static void main(String args[]) {

// create a linked list

LinkedList ll = new LinkedList();

// add elements to the linked list

ll.add("F");

ll.add("B");

ll.add("D");

ll.add("E");

ll.add("C");

ll.addLast("Z");

ll.addFirst("A");

ll.add(1, "A2");

System.out.println("Original contents of ll: " + ll);

// remove elements from the linked list

ll.remove("F");

ll.remove(2);

System.out.println("Contents of ll after deletion: " + ll);

// remove first and last elements

ll.removeFirst();

ll.removeLast();

System.out.println("ll after deleting first and last: " + ll);

// get and set a value

Object val = ll.get(2);

ll.set(2, (String) val + " Changed");

System.out.println("ll after change: " + ll);

}

This will produce the following result −

Output

Original contents of ll: [A, A2, F, B, D, E, C, Z]

Contents of ll after deletion: [A, A2, D, E, C, Z]

ll after deleting first and last: [A2, D, E, C]

ll after change: [A2, D, E Changed, C]

1.4 Stacks

1.5 Queues

1.6 Set

A Set is a Collection that cannot contain duplicate elements. It models the mathematical set abstraction.

The Set interface contains only methods inherited from Collection and adds the restriction that duplicate elements are prohibited.

Set also adds a stronger contract on the behavior of the equals and hashCode operations, allowing Set instances to be compared meaningfully even if their implementation types differ.

The methods declared by Set are summarized in the following table −

Sr.No.	Method & Description
1	add( ) Adds an object to the collection.
2	clear( ) Removes all objects from the collection.
3	contains( ) Returns true if a specified object is an element within the collection.
4	isEmpty( ) Returns true if the collection has no elements.
5	iterator( ) Returns an Iterator object for the collection, which may be used to retrieve an object.
6	remove( ) Removes a specified object from the collection.
7	size( ) Returns the number of elements in the collection.

Example

Set has its implementation in various classes like HashSet, TreeSet, LinkedHashSet. Following is an example to explain Set functionality −

Live Demo

import java.util.*;

public class SetDemo {

public static void main(String args[]) {

int count[] = {34, 22,10,60,30,22};

Set<Integer> set = new HashSet<Integer>();

try {

for(int i = 0; i < 5; i++) {

set.add(count[i]);

}

System.out.println(set);

TreeSet sortedSet = new TreeSet<Integer>(set);

System.out.println("The sorted list is:");

System.out.println(sortedSet);

System.out.println("The First element of the set is: "+ (Integer)sortedSet.first());

System.out.println("The last element of the set is: "+ (Integer)sortedSet.last());

}

catch(Exception e) {}

}

This will produce the following result −

Output

[34, 22, 10, 60, 30]

The sorted list is:

[10, 22, 30, 34, 60]

The First element of the set is: 10

The last element of the set is: 60

1.7 TreeSet

TreeSet provides an implementation of the Set interface that uses a tree for storage. Objects are stored in a sorted and ascending order.

Access and retrieval times are quite fast, which makes TreeSet an excellent choice when storing large amounts of sorted information that must be found quickly.

Following is the list of the constructors supported by the TreeSet class.

Sr.No.	Constructor & Description
1	TreeSet( ) This constructor constructs an empty tree set that will be sorted in an ascending order according to the natural order of its elements.
2	TreeSet(Collection c) This constructor builds a tree set that contains the elements of the collection c.
3	TreeSet(Comparator comp) This constructor constructs an empty tree set that will be sorted according to the given comparator.
4	TreeSet(SortedSet ss) This constructor builds a TreeSet that contains the elements of the given SortedSet.

Apart from the methods inherited from its parent classes, TreeSet defines the following methods −

Sr.No.	Method & Description
1	void add(Object o) Adds the specified element to this set if it is not already present.
2	boolean addAll(Collection c) Adds all of the elements in the specified collection to this set.
3	void clear() Removes all of the elements from this set.
4	Object clone() Returns a shallow copy of this TreeSet instance.
5	Comparator comparator() Returns the comparator used to order this sorted set, or null if this tree set uses its elements natural ordering.
6	boolean contains(Object o) Returns true if this set contains the specified element.
7	Object first() Returns the first (lowest) element currently in this sorted set.
8	SortedSet headSet(Object toElement) Returns a view of the portion of this set whose elements are strictly less than toElement.
9	boolean isEmpty() Returns true if this set contains no elements.
10	Iterator iterator() Returns an iterator over the elements in this set.
11	Object last() Returns the last (highest) element currently in this sorted set.
12	boolean remove(Object o) Removes the specified element from this set if it is present.
13	int size() Returns the number of elements in this set (its cardinality).
14	SortedSet subSet(Object fromElement, Object toElement) Returns a view of the portion of this set whose elements range from fromElement, inclusive, to toElement, exclusive.
15	SortedSet tailSet(Object fromElement) Returns a view of the portion of this set whose elements are greater than or equal to fromElement.

Example

The following program illustrates several of the methods supported by this collection −

Live Demo

import java.util.*;

public class TreeSetDemo {

public static void main(String args[]) {

// Create a tree set

TreeSet ts = new TreeSet();

// Add elements to the tree set

ts.add("C");

ts.add("A");

ts.add("B");

ts.add("E");

ts.add("F");

ts.add("D");

System.out.println(ts);

}

This will produce the following result −

Output

[A, B, C, D, E, F]

1.8 Binary Search Tree (BST)

A Binary Search Tree (BST) is a tree in which all the nodes follow the below-mentioned properties −

· The left sub-tree of a node has a key less than or equal to its parent node's key.

· The right sub-tree of a node has a key greater than to its parent node's key.

Thus, BST divides all its sub-trees into two segments; the left sub-tree and the right sub-tree and can be defined as −

left_subtree (keys) ≤ node (key) ≤ right_subtree (keys)

Basic Operations

Following are the basic operations of a tree −

· Search − Searches an element in a tree.

· Insert − Inserts an element in a tree.

· Pre-order Traversal − Traverses a tree in a pre-order manner.

· In-order Traversal − Traverses a tree in an in-order manner.

· Post-order Traversal − Traverses a tree in a post-order manner.

Node

Define a node having some data, references to its left and right child nodes.

struct node {

int data;

struct node *leftChild;

struct node *rightChild;

};

Search Operation

Whenever an element is to be searched, start searching from the root node. Then if the data is less than the key value, search for the element in the left subtree. Otherwise, search for the element in the right subtree. Follow the same algorithm for each node.

Algorithm

struct node* search(int data){

struct node *current = root;

printf("Visiting elements: ");

while(current->data != data){

if(current != NULL) {

printf("%d ",current->data);

//go to left tree

if(current->data > data){

current = current->leftChild;

} //else go to right tree

else {

current = current->rightChild;

}

//not found

if(current == NULL){

return NULL;

}

return current;

}

Insert Operation

Whenever an element is to be inserted, first locate its proper location. Start searching from the root node, then if the data is less than the key value, search for the empty location in the left subtree and insert the data. Otherwise, search for the empty location in the right subtree and insert the data.

Algorithm

void insert(int data) {

struct node *tempNode = (struct node*) malloc(sizeof(struct node));

struct node *current;

struct node *parent;

tempNode->data = data;

tempNode->leftChild = NULL;

tempNode->rightChild = NULL;

//if tree is empty

if(root == NULL) {

root = tempNode;

} else {

current = root;

parent = NULL;

while(1) {

parent = current;

//go to left of the tree

if(data < parent->data) {

current = current->leftChild;

//insert to the left

if(current == NULL) {

parent->leftChild = tempNode;

return;

}

} //go to right of the tree

else {

current = current->rightChild;

//insert to the right

if(current == NULL) {

parent->rightChild = tempNode;

return;

}

1.9 Heap (Max Heap/Min Heap)

Heap represents a special tree based data structure used to represent priority queue or for heap sort. We'll going to discuss binary heap tree specifically.

Binary heap tree can be classified as a binary tree with two constraints:

· Completeness - Binary heap tree is a complete binary tree except the last level which may not have all elements but elements from left to right should be filled in.

· Heapness - All parent nodes should be greater or smaller to their children. If parent node is to be greater than its child then it is called Max heap otherwise it is called Min heap. Max heap is used for heap sort and Min heap is used for priority queue. We're considering Min Heap and will use array implementation for the same.

Basic Operations

Following are basic primary operations of a Min heap which are following.

· Insert - insert an element in a heap.

· Get Minimum - get minimum element from the heap.

· Remove Minimum - remove the minimum element from the heap

Insert Operation

· Whenever an element is to be inserted. Insert element at the end of the array. Increase the size of heap by 1.

· Heap up the element while heap property is broken. Compare element with parent's value and swap them if required.

void insert(int value) {

size++;

intArray[size - 1] = value;

heapUp(size - 1);

}

void heapUp(int nodeIndex){

int parentIndex, tmp;

if (nodeIndex != 0) {

parentIndex = getParentIndex(nodeIndex);

if (intArray[parentIndex] > intArray[nodeIndex]) {

tmp = intArray[parentIndex];

intArray[parentIndex] = intArray[nodeIndex];

intArray[nodeIndex] = tmp;

heapUp(parentIndex);

}

Get Minimum

Get the first element of the array implementing the heap being root.

int getMinimum(){

return intArray[0];

}

Remove Minimum

· Whenever an element is to be removed. Get the last element of the array and reduce size of heap by 1.

· Heap down the element while heap property is broken. Compare element with children's value and swap them if required.

void removeMin() {

intArray[0] = intArray[size - 1];

size--;

if (size > 0)

heapDown(0);

}

void heapDown(int nodeIndex){

int leftChildIndex, rightChildIndex, minIndex, tmp;

leftChildIndex = getLeftChildIndex(nodeIndex);

rightChildIndex = getRightChildIndex(nodeIndex);

if (rightChildIndex >= size) {

if (leftChildIndex >= size)

return;

else

minIndex = leftChildIndex;

} else {

if (intArray[leftChildIndex] <= intArray[rightChildIndex])

minIndex = leftChildIndex;

else

minIndex = rightChildIndex;

}

if (intArray[nodeIndex] > intArray[minIndex]) {

tmp = intArray[minIndex];

intArray[minIndex] = intArray[nodeIndex];

intArray[nodeIndex] = tmp;

heapDown(minIndex);

}

Demo Program

HeapDemo.c

#include <stdio.h>

#include <string.h>

#include <stdlib.h>

#include <stdbool.h>

int intArray[10];

int size;

bool isEmpty(){

return size == 0;

}

int getMinimum(){

return intArray[0];

}

int getLeftChildIndex(int nodeIndex){

return 2*nodeIndex +1;

}

int getRightChildIndex(int nodeIndex){

return 2*nodeIndex +2;

}

int getParentIndex(int nodeIndex){

return (nodeIndex -1)/2;

}

bool isFull(){

return size == 10;

}

/**

* Heap up the new element,until heap property is broken.

* Steps:

* 1. Compare node's value with parent's value.

* 2. Swap them, If they are in wrong order.

* */

void heapUp(int nodeIndex){

int parentIndex, tmp;

if (nodeIndex != 0) {

parentIndex = getParentIndex(nodeIndex);

if (intArray[parentIndex] > intArray[nodeIndex]) {

tmp = intArray[parentIndex];

intArray[parentIndex] = intArray[nodeIndex];

intArray[nodeIndex] = tmp;

heapUp(parentIndex);

}

/**

* Heap down the root element being least in value,until heap property is broken.

* Steps:

* 1.If current node has no children, done.

* 2.If current node has one children and heap property is broken,

* 3.Swap the current node and child node and heap down.

* 4.If current node has one children and heap property is broken, find smaller one

* 5.Swap the current node and child node and heap down.

* */

void heapDown(int nodeIndex){

int leftChildIndex, rightChildIndex, minIndex, tmp;

leftChildIndex = getLeftChildIndex(nodeIndex);

rightChildIndex = getRightChildIndex(nodeIndex);

if (rightChildIndex >= size) {

if (leftChildIndex >= size)

return;

else

minIndex = leftChildIndex;

} else {

if (intArray[leftChildIndex] <= intArray[rightChildIndex])

minIndex = leftChildIndex;

else

minIndex = rightChildIndex;

}

if (intArray[nodeIndex] > intArray[minIndex]) {

tmp = intArray[minIndex];

intArray[minIndex] = intArray[nodeIndex];

intArray[nodeIndex] = tmp;

heapDown(minIndex);

}

void insert(int value) {

size++;

intArray[size - 1] = value;

heapUp(size - 1);

}

void removeMin() {

intArray[0] = intArray[size - 1];

size--;

if (size > 0)

heapDown(0);

}

main()

{

/* 5 //Level 0

insert(5);

/* 1 //Level 0

* |

* 5---| //Level 1

insert(1);

/* 1 //Level 0

* |

* 5---|---3 //Level 1

insert(3);

/* 1 //Level 0

* |

* 5---|---3 //Level 1

* |

* 8--| //Level 2

insert(8);

/* 1 //Level 0

* |

* 5---|---3 //Level 1

* |

* 8--|--9 //Level 2

insert(9);

/* 1 //Level 0

* |

* 5---|---3 //Level 1

* | |

* 8--|--9 6--| //Level 2

insert(6);

/* 1 //Level 0

* |

* 5---|---2 //Level 1

* | |

* 8--|--9 6--|--3 //Level 2

insert(2);

printf("%d", getMinimum());

removeMin();

/* 2 //Level 0

* |

* 5---|---3 //Level 1

* | |

* 8--|--9 6--| //Level 2

printf("\n%d", getMinimum());

}

If we compile and run the above program then it would produce following result:

1.10 Graph

A graph is an abstract notation used to represent the connection between pairs of objects. A graph consists of −

· Vertices − Interconnected objects in a graph are called vertices. Vertices are also known as nodes.

· Edges − Edges are the links that connect the vertices.

There are two types of graphs −

· Directed graph − In a directed graph, edges have direction, i.e., edges go from one vertex to another.

· Undirected graph − In an undirected graph, edges have no direction.

Graph Coloring

Graph coloring is a method to assign colors to the vertices of a graph so that no two adjacent vertices have the same color. Some graph coloring problems are −

· Vertex coloring − A way of coloring the vertices of a graph so that no two adjacent vertices share the same color.

· Edge Coloring − It is the method of assigning a color to each edge so that no two adjacent edges have the same color.

· Face coloring − It assigns a color to each face or region of a planar graph so that no two faces that share a common boundary have the same color.

Chromatic Number

Chromatic number is the minimum number of colors required to color a graph. For example, the chromatic number of the following graph is 3.

The concept of graph coloring is applied in preparing timetables, mobile radio frequency assignment, Suduku, register allocation, and coloring of maps.

Steps for graph coloring

· Set the initial value of each processor in the n-dimensional array to 1.

· Now to assign a particular color to a vertex, determine whether that color is already assigned to the adjacent vertices or not.

· If a processor detects same color in the adjacent vertices, it sets its value in the array to 0.

· After making n² comparisons, if any element of the array is 1, then it is a valid coloring.

Pseudocode for graph coloring

begin

create the processors P(i₀,i₁,...i_n_-₁) where 0_i_v < m, 0 _ v < n

status[i0,..i_n_-₁] = 1

for j varies from 0 to n-1 do

begin

for k varies from 0 to n-1 do

begin

if a_j_,_k=1 and i_j=i_kthen

status[i₀,..i_n_-₁] =0

end

ok = ΣStatus

if ok > 0, then display valid coloring exists

else

display invalid coloring

end

Minimal Spanning Tree

A spanning tree whose sum of weight (or length) of all its edges is less than all other possible spanning tree of graph G is known as a minimal spanning tree or minimum cost spanning tree.

To implement the minimum cost-spanning tree, the following two methods are used −

· Prim’s Algorithm

· Kruskal’s Algorithm

Prim's Algorithm

Prim’s algorithm is a greedy algorithm, which helps us find the minimum spanning tree for a weighted undirected graph. It selects a vertex first and finds an edge with the lowest weight incident on that vertex.

Steps of Prim’s Algorithm

· Select any vertex, say v₁ of Graph G.

· Select an edge, say e₁ of G such that e₁ = v₁ v₂ and v₁ ≠ v₂ and e₁ has minimum weight among the edges incident on v₁ in graph G.

· Now, following step 2, select the minimum weighted edge incident on v₂.

· Continue this till n–1 edges have been chosen. Here n is the number of vertices. Kruskal's Algorithm

Kruskal’s algorithm is a greedy algorithm, which helps us find the minimum spanning tree for a connected weighted graph, adding increasing cost arcs at each step. It is a minimum-spanning-tree algorithm that finds an edge of the least possible weight that connects any two trees in the forest.

Steps of Kruskal’s Algorithm

· Select an edge of minimum weight; say e₁ of Graph G and e₁ is not a loop.

· Select the next minimum weighted edge connected to e₁.

· Continue this till n–1 edges have been chosen. Here n is the number of vertices. Shortest Path Algorithm

Shortest Path algorithm is a method of finding the least cost path from the source node(S) to the destination node (D). Here, we will discuss Moore’s algorithm, also known as Breadth First Search Algorithm.

Moore’s algorithm

· Label the source vertex, S and label it i and set i=0.

· Find all unlabeled vertices adjacent to the vertex labeled i. If no vertices are connected to the vertex, S, then vertex, D, is not connected to S. If there are vertices connected to S, label them i+1.

· If D is labeled, then go to step 4, else go to step 2 to increase i=i+1.

· Stop after the length of the shortest path is found.

In this section we will see different traversal algorithms to traverse keys present in binary search tree. These traversals are Inorder traversal, Preorder traversal, Postorder traversal and the level order traversal.

Suppose we have one tree like this −

The Inorder traversal sequence will be like − 5 8 10 15 16 20 23

The Preorder traversal sequence will be like − 10 5 8 16 15 20 23

The Postorder traversal sequence will be like − 8 5 15 23 20 16 10

The Level-order traversal sequence will be like − 10, 5, 16, 8, 15, 20, 23

Algorithm

inorderTraverse(root):

Begin

if root is not empty, then

inorderTraversal(left of root)

print the value of root

inorderTraversal(right of root)

end if

End

preorderTraverse(root):

Begin

if root is not empty, then

print the value of root

preorderTraversal(left of root)

preorderTraversal(right of root)

end if

End

postorderTraverse(root):

Begin

if root is not empty, then

postorderTraversal(left of root)

postorderTraversal(right of root)

print the value of root

end if

End

levelOrderTraverse(root):

Begin

define queue que to store nodes

insert root into the que.

while que is not empty, do

item := item present at front position of queue

print the value of item

if left of the item is not null, then

insert left of item into que

end if

if right of the item is not null, then

insert right of item into que

end if

delete front element from que

done

End

Example

#include<iostream>

#include<queue>

using namespace std;

class node{

public:

int h_left, h_right, bf, value;

node *left, *right;

};

class tree{

private:

node *get_node(int key);

public:

node *root;

tree(){

root = NULL; //set root as NULL at the beginning

}

void inorder_traversal(node *r);

void preorder_traversal(node *r);

void postorder_traversal(node *r);

void levelorder_traversal(node *r);

node *insert_node(node *root, int key);

};

node *tree::get_node(int key){

node *new_node;

new_node = new node; //create a new node dynamically

new_node->h_left = 0; new_node->h_right = 0;

new_node->bf = 0;

new_node->value = key; //store the value from given key

new_node->left = NULL; new_node->right = NULL;

return new_node;

}

void tree::inorder_traversal(node *r){

if(r != NULL){ //When root is present, visit left - root - right

inorder_traversal(r->left);

cout << r->value << " ";

inorder_traversal(r->right);

}

void tree::preorder_traversal(node *r){

if(r != NULL){ //When root is present, visit left - root - right

cout << r->value << " ";

preorder_traversal(r->left);

preorder_traversal(r->right);

}

void tree::postorder_traversal(node *r){

if(r != NULL){ //When root is present, visit left - root - right

postorder_traversal(r->left);

postorder_traversal(r->right);

cout << r->value << " ";

}

void tree::levelorder_traversal(node *root){

queue <node*> que;

node *item;

que.push(root); //insert the root at first

while(!que.empty()){

item = que.front(); //get the element from the front end

cout << item->value << " ";

if(item->left != NULL) //When left child is present, insert into queue

que.push(item->left);

if(item->right != NULL) //When right child is present, insert into queue

que.push(item->right);

que.pop(); //remove the item from queue

}

node *tree::insert_node(node *root, int key){

if(root == NULL){

return (get_node(key)); //when tree is empty, create a node as root

}

if(key < root->value){ //when key is smaller than root value, go to the left

root->left = insert_node(root->left, key);

}else if(key > root->value){ //when key is greater than root value, go to the right

root->right = insert_node(root->right, key);

}

return root; //when key is already present, do not insert it again

}

main(){

node *root;

tree my_tree;

//Insert some keys into the tree.

my_tree.root = my_tree.insert_node(my_tree.root, 10);

my_tree.root = my_tree.insert_node(my_tree.root, 5);

my_tree.root = my_tree.insert_node(my_tree.root, 16);

my_tree.root = my_tree.insert_node(my_tree.root, 20);

my_tree.root = my_tree.insert_node(my_tree.root, 15);

my_tree.root = my_tree.insert_node(my_tree.root, 8);

my_tree.root = my_tree.insert_node(my_tree.root, 23);

cout << "In-Order Traversal: ";

my_tree.inorder_traversal(my_tree.root);

cout << "\nPre-Order Traversal: ";

my_tree.preorder_traversal(my_tree.root);

cout << "\nPost-Order Traversal: ";

my_tree.postorder_traversal(my_tree.root);

cout << "\nLevel-Order Traversal: ";

my_tree.levelorder_traversal(my_tree.root);

}

Output

In-Order Traversal: 5 8 10 15 16 20 23

Pre-Order Traversal: 10 5 8 16 15 20 23

Post-Order Traversal: 8 5 15 23 20 16 10

Level-Order Traversal: 10 5 16 8 15 20 23

2.4 Breadth-First Search

Breadth First Search or BFS for a Graph

The Breadth First Search (BFS) traversal is an algorithm, which is used to visit all of the nodes of a given graph. In this traversal algorithm one node is selected and then all of the adjacent nodes are visited one by one. After completing all of the adjacent vertices, it moves further to check another vertices and checks its adjacent vertices again.

To implement this algorithm, we need to use the Queue data structure. All the adjacent vertices are added into the queue, when all adjacent vertices are completed, one item is removed from the queue and start traversing through that vertex again.

In Graph sometimes, we may get some cycles, so we will use an array to mark when a node is visited already or not.

Input - The Adjacency matrix of the graph.

A B C D E F

A 0 1 1 1 0 0

B 1 0 0 1 1 0

C 1 0 0 1 0 1

D 1 1 1 0 1 1

E 0 1 0 1 0 1

F 0 0 1 1 1 0

Output - BFS Traversal: B A D E C F

Algorithm

bfs(vertices, start)

Input − The list of vertices, and the start vertex.

Output − Traverse all of the nodes, if the graph is connected.

Begin

define an empty queue que

at first mark all nodes status as unvisited

add the start vertex into the que

while que is not empty, do

delete item from que and set to u

display the vertex u

for all vertices 1 adjacent with u, do

if vertices[i] is unvisited, then

mark vertices[i] as temporarily visited

add v into the queue

mark

done

mark u as completely visited

done

End

Example

#include<iostream>

#include<queue>

#define NODE 6

using namespace std;

typedef struct node{

int val;

int state; //status

}node;

int graph[NODE][NODE] = {

{0, 1, 1, 1, 0, 0},

{1, 0, 0, 1, 1, 0},

{1, 0, 0, 1, 0, 1},

{1, 1, 1, 0, 1, 1},

{0, 1, 0, 1, 0, 1},

{0, 0, 1, 1, 1, 0}

};

void bfs(node *vert, node s){

node u;

int i, j;

queue<node> que;

for(i = 0; i<NODE; i++){

vert[i].state = 0; //not visited

}

vert[s.val].state = 1;//visited

que.push(s); //insert starting node

while(!que.empty()){

u = que.front(); //delete from queue and print

que.pop();

cout << char(u.val+'A') << " ";

for(i = 0; i<NODE; i++){

if(graph[i][u.val]){

//when the node is non-visited

if(vert[i].state == 0){

vert[i].state = 1;

que.push(vert[i]);

}

u.state = 2;//completed for node u

}

int main(){

node vertices[NODE];

node start;

char s;

for(int i = 0; i<NODE; i++){

vertices[i].val = i;

}

s = 'B';//starting vertex B

start.val = s-'A';

cout << "BFS Traversal: ";

bfs(vertices, start);

cout << endl;

}

Output

BFS Traversal: B A D E C F

2.5 Depth-First Search

Depth First Search or DFS for a Graph

The Depth First Search (DFS) is a graph traversal algorithm. In this algorithm one starting vertex is given, and when an adjacent vertex is found, it moves to that adjacent vertex first and try to traverse in the same manner.

It moves through the whole depth, as much as it can go, after that it backtracks to reach previous vertices to find new path.

To implement DFS in iterative way, we need to use the stack data structure. If we want to do it recursively, external stacks are not needed, it can be done internal stacks for the recursion calls.

Input: The Adjacency matrix of a graph.

A B C D E F

A 0 1 1 1 0 0

B 1 0 0 1 1 0

C 1 0 0 1 0 1

D 1 1 1 0 1 1

E 0 1 0 1 0 1

F 0 0 1 1 1 0

Output: DFS Traversal: C F E B D A

Algorithm

dfs(vertices, start)

Input − The list of all vertices, and the start node.

Output − Traverse all nodes in the graph.

Begin

initially make the state to unvisited for all nodes

push start into the stack

while stack is not empty, do

pop element from stack and set to u

display the node u

if u is not visited, then

mark u as visited

for all nodes i connected to u, do

if ith vertex is unvisited, then

push ith vertex into the stack

mark ith vertex as visited

done

End

Example

#include<iostream>

#include<stack>

using namespace std;

#define NODE 6

typedef struct node{

int val;

int state; //status

}node;

int graph[NODE][NODE] = {

{0, 1, 1, 1, 0, 0},

{1, 0, 0, 1, 1, 0},

{1, 0, 0, 1, 0, 1},

{1, 1, 1, 0, 1, 1},

{0, 1, 0, 1, 0, 1},

{0, 0, 1, 1, 1, 0}

};

void dfs(node *vertex, node start){

node u;

stack<node> myStack;

for(int i = 0; i<NODE; i++){

vertex[i].state = 0;//not visited

}

myStack.push(start);

while(!myStack.empty()){

//pop and print node

u = myStack.top();

myStack.pop();

cout << char(u.val+'A') << " ";

if(u.state != 1){

//update vertex status to visited

u.state = 1;

vertex[u.val].state = 1;

for(int i = 0; i<NODE; i++){

if(graph[i][u.val]){

if(vertex[i].state == 0){

myStack.push(vertex[i]);

vertex[i].state = 1;

}

int main(){

node vertices[NODE];

node start;

char s;

for(int i = 0; i<NODE; i++){

vertices[i].val = i;

}

s = 'C';//starting vertex C

start.val = s-'A';

cout << "DFS Traversal: ";

dfs(vertices, start);

cout << endl;

}

Output

DFS Traversal: C F E B D A

2.6 Binary Search

Description

The java.util.Arrays.binarySearch(int[] a, int key) method searches the specified array of ints for the specified value using the binary search algorithm.The array must be sorted before making this call.If it is not sorted, the results are undefined.

Declaration

Following is the declaration for java.util.Arrays.binarySearch() method

public static int binarySearch(int[] a, int key)

Parameters

· a − This is the array to be searched.

· key − This is the value to be searched for.

Return Value

This method returns index of the search key, if it is contained in the array, else it returns (-(insertion point) - 1). The insertion point is the point at which the key would be inserted into the array: the index of the first element greater than the key, or a.length if all elements in the array are less than the specified key.

Exception

Example

The following example shows the usage of java.util.Arrays.binarySearch() method.

Live Demo

package com.tutorialspoint;

import java.util.Arrays;

public class ArrayDemo {

public static void main(String[] args) {